반응형
목차
1. 역행렬
2. 역행렬의 성질
3. 2x2행렬의 역행렬
1. 역행렬
(1) 역행렬(inverse matrix)은 정사각행렬의 곱에 대한 역원이다.
정사각행렬 A가 역행렬이 존재하면 A를 가역(invertible)이라고 한다.

(*) 역행렬의 유일성
A가 가역행렬이면 A의 역행렬은 유일하다.
pf) A'와 A''가 A의 역행렬이면 다음이 성립한다.
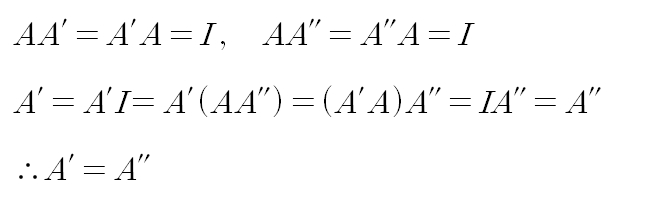
2. 역행렬의 성질
행렬 A는 정사각 행렬이다.
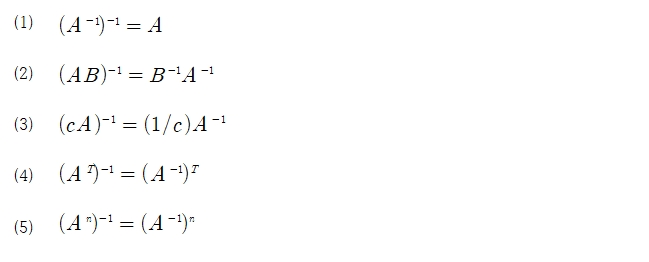
2. 2x2의 역행렬

식에서 알 수 있듯이, 2x2의 행렬일 경우 ad-bc=0 이면 역행렬이 존재한다.
여기서, ad-bc가 2x2행렬의 행렬식이다.
다음 두개의 행렬은 ad-bc가 0이 아니므로 역행렬이 존재하지 않는다.

반응형
'행렬' 카테고리의 다른 글
| 4. 역행렬 구하기 (가우스-조르당) (2) | 2021.12.18 |
|---|---|
| 2. 행렬 대수 성질 (0) | 2020.07.06 |
| 1. 행렬과 행렬 계산법 (0) | 2020.07.04 |


