화살표 벡터는 크기와 방향이 있지만,
화살표가 아닌 임의의 다른 벡터공간의 원소인 벡터는
크기와 방향을 내포하고 있을까?
임의의 벡터가 왜 화살표로 나타내어질까?
1. 대수공간
대수공간이란 어떤 집합과 집합의 원소들에 대해
이항연산이 정의된 수학적 개념입니다.
실수 집합R에 +연산을 정의한다면
이것은 대수공간이며 (R,+)라고 표시합니다.
복소수 집합C에 x연산을 정의하면
(C,x)로 표시하며 이 또한 대수공간입니다.
연산에 대해 "닫혀있다" "열려있다"
항등원과 역원의 존재, 교환법칙, 결합법칙 등의
개념을 중학과정에서 보고 너무나도 쓸떼없다고
생각하신적 다들 있으시지요?
이때까지만 해도 우리는 너무 당연하게 생각했던
위의 개념들이 적용되는 공간은 매우매우 한정적인 것을
대수구조를 배워서야 알게 되죠.
대수구조의 특징에 따라서
(가환)군, 환, 체, 벡터공간 등 으로 나눕니다.
이러한 대수구조를 연구하는 수학의 한 분야를
현대대수학 혹은 추상대수학이라고 합니다.
그 중에서 특별히 선형성(linear)을 가지는
부분을 연구하는 것이 선형대수학입니다.
2. 동형
아라비아숫자(A)와 로마숫자(R)가
서로 대응된다는 것을 잘 알고 있지만
이에 대해서 아무것도 모르는 외계인이
다른 문화권의 문서를 보았다고 합시다.
어떤 나라의 문서에는 다음과 같이 적혀있습니다.
" 2 + 3 = 5 "
다른 나라의 문서에는 다음과 같이 적혀져 있습니다.
" II \ III = V "
이러한 많은 문서들을 연구하고서
외계인은 결론을 냅니다.
"2가 II이고, 3이 III 이고 5가 V이며
+와 \의 연산이 방식 동일하구나"
원소들이 일대일대응이 되며
연산의 방법이 같아서, 연산 후의 결과도 같게 대응 되니,
두 공간의 구조가 같다고 판단합니다.
(A, +) ≃ (R, \)
이를 동형(isomorphic)이라고 합니다.
중요한 점은 표현법만 다를 뿐 구조가 같다는 뜻입니다.
3. 벡터
순서쌍들의 집합에 연산을 정의하여
벡터공간을 만들 수 있습니다.
(a, b) + (c, d) = (a+c, b+d)
k(a, b) = (ka, kb)
이하 생략하며 이 대수구조는
n차원의 순서쌍 R^n에 더하기와 스칼라곱의 연산이
정의된 구조라고 해서 다음과 같이 표기합니다.

화살표들의 집합에도 그림으로 연산을 정의할 수 있습니다.
화살표들의 집합을 위로 향하는 화살표로 정하면
이 대수구조는 다음과 같이 표기할 수 있습니다.


자 그럼, 임의의 화살표를 좌표평면에 올립니다.
시작점은 원점에 올리면
끝 점은 무조건 하나의 순서쌍(좌표)을 가리키게 됩니다.
그 말은, 하나의 화살표가 무조건 하나의 순서쌍에
대응된다는 뜻이죠, 일대일 대응입니다.
또, 화살표들의 합이 순서쌍들의 합으로 나타납니다.
화살표끼리의 합을 한 결과가
곧 화살표 끝점의 좌표 끼리의 합으로
나타나집니다.
화살표의 스칼라배 또한
화살표를 그 스칼라만큼 길게 늘여뜨려
끝 점의 순서쌍을 가리키게 됩니다.
이 또한 순서쌍의 스칼라배와 동일한 결과로 표현될 수 있죠.
즉, 순서쌍의 공간과 화살표의 공간은 동형이 됩니다.

4. 동형사상
동형사상이란 두 동형인 대수구조를
이어주는 사상(함수)입니다.
두 대수구조 A와 B가 동형이라면
어떤 동형사상 f가 존재해서
f : A->B
연산이나 구조의 특징을 전혀 망치지 않고
A를 B의 표기법으로 바꾸어주는 것이죠.
위의 아라비아, 로마자 숫자 표기들을
서로 바꾸어 표현할 수 있는 것이 예입니다.
번역이라고 할 수 있겠네요.

3번에서 보았듯이 순서쌍의 공간과
화살표의 공간은 동형이므로
적절한 동형사상을 통해 표현법만 바꾸어 줄 수 있습니다.
그 동형사상은 쉽게
화살표를 시점을 원점으로 좌표평면에
올리기만 하면 됩니다.
그렇기 때문에 하나의 순서쌍 (2,3)은
원점에서 시작해서 끝점이 (2,3)으로
갈 수 있는 단 하나의 화살표로 대응되는 것입니다.

이로인해서 순서쌍이 화살표로 변하면서(번역되면서)
단 하나의 길이(크기)와 각도(방향)이
생길 수 밖에 없습니다.
우리말을 중국말로 번역해서 말하면
원래 없던 성조가 생기듯이
순서쌍의 벡터를 화살표의 벡터로 동형사상 보내면서
길이와 방향이 생깁니다.
이것은 당연히 두 구조가 표현법만 다를 뿐
구조가 같은 동형이기 때문입니다.
(언어는 동형이 아니지만요 굳이 이해하기 쉬운 예를 들어보려니...)
6. 벡터공간의 동형
차원이 같은 벡터 공간들은 모두 동형입니다.
그래서 순서쌍이 아닌 화살표도 아닌
어떤 해괴망측한 표현법의 벡터공간을 들고와도
적당한 동형사상을 통해 화살표로
만들어 버릴 수 있습니다.
예를 들어서 2차 다항함수들에 덧셈과
스칼라배를 정의하면 이는
3차원 벡터공간이 됩니다.

3차원인 이유는 이것의 기저가 x^2, x, x^0 3개이므로
3차원이며 이것이 벡터공간이 되는지는 전 포스팅의
벡터공간의 정의에 따라 해보시면 됩니다.
2차 함수의 계수들만 따서 순서쌍으로 만들면
아래와 같이 일대일대응이며, 연산의 보존, 구조의
보존을 보여주며 동형입니다.

순서쌍은 또한 화살표 공간과 동형이니
저 2차 함수들의 벡터공간 또한 화살표로 번역할 수 있습니다.
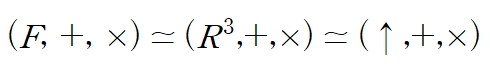
7. 정리
같은 차원의 모든 벡터공간은 서로 동형이기 때문에
번역할 수 있는 동형사상이 존재한다.
따라서 n차원 벡터공간의 원소는 무조건
n차원의 유클리드 공간에서의 화살표로 나타낼 수 있다.