반응형
선형미분방정식이라 함은 다음과 같은 형식을 말한다.

선형미분방정식 중에서 y의 이계도함수까지만 포함하는, 2계선형미분방정식을 다룬다.
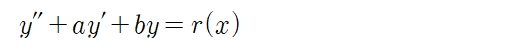
2계 선형미분방정식의 풀이법에는 크게 2가지 방법 (론스키안행렬식, 미정계수법)이 있는데 이 글에서는
미정계수법을 이용한 미분방정식의 풀이에 대해 쓴 글이다.
미정계수법의 풀이를 보이기 전에, 일반해를 알아야 하고 동차선형미분방정식 ( 쉽게 말해서 r(x)가 없는 식 ) 의 풀이를
먼저 알아야 한다. 2계 동차미분방정식의 해는 다음과 같다.
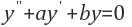
의 특성방정식 의 두 근 에 대해

이다.
(m,n은 음이 아닌 정수. e^(ax), e^(bx)가 서로 독립이라면 m과 n은 0 으로 두자)
여기에 특수해를 더해주면 선형미분방정식의 해가 나오게 된다. 특수해를 구해주기 위해서 미정계수법을 사용한다.

(출처 : 위키백과)
r(x)의 형태에 따라 y_p를 선택해주고 만약 y_p가 동차미분방정식의 해가 된다면 y_p에 x를 하나씩 곱해준다.
일반해와 특수해를 더해주면 미분방정식의 해가 된다.



r(x)=x^2 이므로 미정계수법을 사용하여 특수해의 꼴을 밑과 같이 둔다.

y_p를 미분방정식에 대입하여 a,b,c를 구한다.
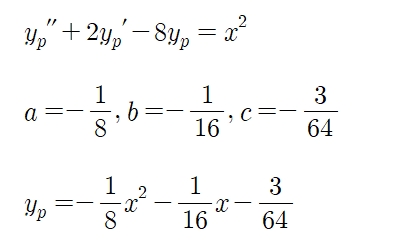
미분방정식의 해는 일반해와 특수해를 더하면 되므로,

반응형